We now consider visual languages that can create code. In looking at
a broad set of languages, we find that some concepts are especially difficult
to represent visually. Repetition, whether through iteration or recursion,
can be hard to communicate. Parameter passing is also difficult; the textual
substitution of a parameter does not lend itself to simple visual representation.
The representations of repetition or parameters differ according to the
underlying language model. We distinguish between imperative and functional
languages; we look at one functional language, PROGRAPH, in depth.
Many of the visualization tools we discussed in the previous sections
are based around imperative languages. And all flowchart techniques are
diagrammatic descriptions of imperative languages.
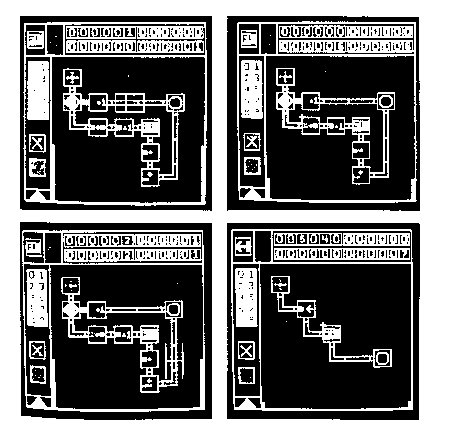
PICT is a system developed by Glinert in his Ph.D. dissertation (1985). He strives for a system in which no text will be necessary.
Figure 2.50. PICT factorial example. From Glinert (1985).
The prototype is very restricted; only four 6-digit nonnegative decimal
integers are allowed in each module. This essentially solves the parameter-passing
problem. Each of the variables is assigned a color. The whole language
is defined as
|
<language primitive> |
::= |
<sys control | <declarative op> | <boolean op> |
|
<sys control> |
::= |
'start(entry)' | 'stop/return' |
|
<declarative op> |
::= |
+ | - | + 1 | - 1 | set to 1 | set to 0 | assign a copy | input from joystick |
|
<boolean op> |
::= |
> | = | < | = 0 | = 1 |
Glinert writes:
PICT/D user programs look like flowcharts; although some professionals
have questioned the usefulness of these diagrams, we find much to recommend
the flowchart when it is the program itself rather than merely an
aid to documenting it (page 53).
Using flowchart-like symbols, if and while statements can be constructed.
Figure 2.51. PICT conditionals and loops. From Glinert (1985).
The physical construction of the program is done with a joystick, so the loops are drawn by steering a line around the screen.
Blox (Glinert 1986) is a visual programming language made up of puzzle-like pieces that fit together.
Figure 2.52. Blox. From Glinert (1986).
Protrusions are fit into sockets on the pieces, which consist of program
language statements such as while and if statements. Each
piece can hide lower level constructs that are encapsulated within. (This
is the H-graph component of the language.) The individual statements such
as assignments, are typed in at the keyboard. Notable in the language is
the way then and else clauses move off the main vertical
line of the control.
Functional languages seem by their nature to lend themselves to visual
representation. Most often, they have simple, uniform data structures.
They do not have parameter passing, and they don't allow multiple assignment.
This means that the data flow graphs previously described can be used for
creating low level expressions. At the higher level, functional languages
provide a set of functional forms, which allow for the combining of already
defined functions. The function becomes an object that can be manipulated
to form a higher-level function.
Once a value is determined in a functional system, that value flows
through the rest of the system unchanged. This is called the principle
of single assignment. In practice, this is very restrictive, and many languages
relax this restriction in order to handle iteration in a nonrecursive manner.
In the textual data flow language Val, one can increment a designated loop
variable. In textual Sisal, one also has mechanism for incrementing a loop
variable. We see these ideas carry over into visual languages discussed
below.
PROGRAPH (Matwin 1985) is a data flow-like language. Matwin writes:
... graphical formulation of programs in PROGRAPH is based on a premise
that non-linear concepts can be better expressed in a two-dimensional pictorial
form rather than in sequential verbal script.
Here is a simple PROGRAPH program:
Figure 2.53. PROGRAPH square program. From Matwin (1985).
The line coming into the top of the box DEF SQUARE is the function's
input. The line coming out of the box is the result. The branching of the
input line feeds two identical values into the binary multiply function.
SQUARE is used in the procedure VARIANT, which reads two numbers in, computes
their squares, and adds the results together for display. Subroutine calls
assume that the calling routine has the same number of input and output
wires as the called routine.
Here are two examples of conditionals.
Figure 2.54. PROGRAPH conditionals. From Matwin (1985).
In all cases there is a boolean condition box. If the box tests positive,
the THEN box is executed. In the case of the function ABSOLUTE, a number
flows into the function; if the number is less than 0, the number goes
through a unary minus function, converting the number into a positive number.
This number flows out the bottom of the function. If the number is >
0, the IF condition fails, and the number that flowed into the box flows
out unchanged.
In the function MAX, we see the use of another PROGRAPH wiring convention.
An input can be grounded by terminating it with a small, filled square.
If the first input is greater than the second input, the first input flows
through, the second is terminated. Otherwise, the first is terminated,
and the second flows through. Note that even though PROGRAPH does not have
named parameters, the order of the wires performs the same function as
parameter labeling does in textual languages.
Here is a common example from list processing, REVERSE.
Figure 2.55. PROGRAPH reverse. From Matwin (1985).
FIRST and REST correspond to LISP CAR and CDR, but APPEND is slightly
different - it concatenates an element, not a list, on to the back of an
input list. The recursion is accomplished by labeling a box inside the
function with the name REVERSE. The inside of this interior box could be
drawn as a smaller copy of the surrounding box. In such a case we would
get a common visual metaphor for recursion, a picture within a picture,
regressing all the way down to the boundary condition. In textual languages,
the function translates to:
reverse(x)
if (nonempty(x) is TRUE)
return(append(reverse(rest(x)), first(x)))
else return(NIL)
Both the visual and the textual versions are fairly simple;
however the visual version, through the crossing lines in the THEN box,
draws attention to the basic idea of the algorithm.
Unlike most visual functional languages, PROGRAPH supplies an iteration
mechanism. A logical compartment sits on top of a transformation compartment.
In a flow chart, the lines would be drawn explicitly. In PROGRAPH, the
lines are implied. When the condition in the logical compartment is filled,
data is passed to the transformation compartment. Results are then transferred
back to the logical compartment. Even though lines are not drawn back up,
the effect is very much like that of a flow chart, where a line is drawn
explicitly back to the condition box.
Constant initialization is introduced in this figure:
Figure 2.56. PROGRAPH factorial. From Matwin (1985).
The number 1 over the WHILE box is in effect only on the first test; from then on, the line has the value of the leftmost output of the DO loop. This line in effect accumulates the result. On the right side of the DO loop, the input number is decrement by one. This decremented number is output from the DO loop, then grounded. This means the number is fed back into the input line of the WHILE check, but stays internal to the
FACTORIAL box.
Psuedocode for this function reads
factorial (x)
result = 1
while (x >= 2)
result = result * x
x = x - 1
return(result)
Again, both the textual and the visual functions are fairly simple. The visual function needs no temporary variables. However, the introduction of an initialization of a line, and the implicit looping of the construct, make the representation difficult to decipher in a glance. A more complicated example is shown in this figure, a function for merging sorted lists.
Figure 2.57. PROGRAPH merge. From Matwin (1985).
The function uses three sub-functions, relying at the
bottom level on CONCAT, the equivalent of LISP APPEND. Another new convention
is introduced; an arrow on an in wire indicates the wire extends to the
bottom. Notice this convention is necessary as a result of two other conventions
- first, the order the lines exit a function is significant, and second,
lines touching boxes is significant. The THEN box, without the arrow convention,
would have needed to snake the second line around the boxes, and then out
the bottom of the function.
The following is a textual algorithm for merging, in the
SCHEME dialect of LISP, from Abelson (1985). It is recursive, not iterative:
(define (merge s1 s2)
(cond (( empty-stream? s1) s2)
( empty-stream? s2) s1)
else
let ((h1 (head s1))
(h2 (head s2)))
cond ((< h1 h2) (cons-stream h1 ( merge (tail s1) s2)))
((> h1 h2) (cons-stream h2 ( merge s1 (tail s2))))
(else
(cons-stream h1
(merge (tail s1) (tail s2)))))))
The typography is visually aligned, making it is easy
to see the minor difference in the way the (< h1 h2) and ( >h1 h2)
conditions are handled. As it is, the textual version seems easier to understand
than the visual PROGRAPH version. The problem may be in the way the IF,
THEN and ELSE clauses are stacked in the PROGRAPH version. If they were
all drawn side-by-side, and the THEN clause was drawn the same size as
the ELSE clause, the visual version would be somewhat clearer.
PROGRAPH includes a convention for handling operations on lists in parallel. If an input line has a horizontal thick bar attached, then the input is considered multiple. This convention is used in conjunction with the APPLY TO ALL function.
Figure 2.58. PROGRAPH matrix multiply. From Matwin (1985).
Two vectors are fed in as multiples to the APPLY TO ALL function. The
corresponding elements of each vector are added together, and the resulting
list output. In the right-hand diagram, one list is fed in normally, the
other as a multiple. Each sublist of the multiple input will be multiplied
by the single list fed in on the left input line.
Above, matrix multiplication is defined. At the bottom of the second
box, a multiple is fed into a PLUS operation. When single multiples are
fed into PLUS, TIMES, AND, OR, the result is a reduction. So in this example,
the numbers in the list are added together, producing a single number.
Matrices in PROGRAPH as represented as a list of lists. In following
the logic of the matrix multiplication, attention must be paid to which
in wires are multiples. Initially, the left matrix is treated as
a multiple; this means that a row at a time is processed against the entire
transposed right matrix. For every one of the left rows, we treat the right
matrix as a multiple. This means that we multiply row 1 by column 1, then
row 1 by column 2, etc. The third box performs this multiply, and the bottom
of the second box performs the addition. By the sequence of multiples,
we end up constructing an output of lists of lists in the correct order.
This does not seem to be an extremely intuitive way of writing a matrix-multiplication function. However, it does work without named parameters, subscripts, or temporary variables.
Figure 2.59. PROGRAPH find subtree. From Matwin (1985).
In this figure a recursive algorithm for finding a subtree is shown.
The tree itself is treated as a multiple (it is fed in as list of nested
lists). The tree to be matched is also fed in. The APPLY TO ALL function
serves to supply the set of subtrees of the list to the recursive call
in the THEN clause. A multiple OR at the end catches any successful find.
Matwin notes that the OR can be implemented using lazy evaluation.
Figure 2.60. Show and Tell. From Gillet (1986).
Show-and-Tell (Gillet 1986) solves the iteration problem by using the
conventions of a textual data flow language, Lucid. In Lucid, a sequence
of values is kept for each variable. This historical sequence can be referenced
the same way an array can be referenced. Ambler (1989) calls this a temporally-dependent
iteration construct.
Show-and-Tell spatializes this idea by unfolding the multiple instances
of a variable, accordion style. Show-and-Tell contains another interesting
characteristic. If contiguous boxes have conflicting values, they are considered
inconsistent. However, the inconsistency is isolated to the containing
box.
Raeder, in his Ph.D. dissertation (1984) describes his system, which
uses FP as its main model. Raeder writes:
... the strict sequentiality of the imperative model is not compatible with pictures, where there is usually no sequential order imposed on various picture elements visible in a two-dimensional plane (p 104).
A function is defined by drawing a picture of the functions input data,
the functions output data and the actions on the data. The underlying convention
here is the data flow graph. The higher level of abstraction will be an
iconic picture of the function. Then FP-style functional forms are used
to combine functions.
Figure 2.61. Programming in Pictures. From Raeder (1984).
A typing mechanism is added; this is outside of the FP model.
Pagan (1977) describes a visual version of FP.
Figure 2.62. Visual FP. Pagan (1977)
It is different in appearance from the other functional languages we
have just looked at. Instead of using data flow graphs as the visual conventions,
it uses a modification of Nassi-Shneiderman charts. The box-shapes in Nassi-Shneiderman
diagrams represent control structures; in graphical FP they represent different
functional combining forms. The six combining forms are:
constant - rectangular box
construction - two side by side, slab above
composition - one above the other
insert - box within a box, 2 corners connect
apply to all - box in box, criss-cross
condition - arrow.
The system is very simple. As with other Nassi-Schneiderman based systems,
text still predominates much of the representation. However, some of the
linear terseness of the functional forms of FP seems to have been relieved
by the 2-dimensional representation.
Our analysis has not been exhaustive; there are many other systems that are documented and discussed in the literature. We mention briefly some of the systems that often are cited.
Lakin (1986) describes a LISP system in which expressions have been replaced by graphics using the convention of enclosure. It is a variation on a parse tree. The functions themselves are encoded as different enclosing shapes.
Figure 2.63. An enclosure convention for lisp. From Lakin (1986).
Reiss (1987) describes a system for building visual languages. In a sense it is a meta-visual programming language. The system is shown building an FSA language, a flowchart language, and a data flow language. The underlying language is LISP. The pictures can be executed.
Figure 2.64. Garden. From Reiss (1987).