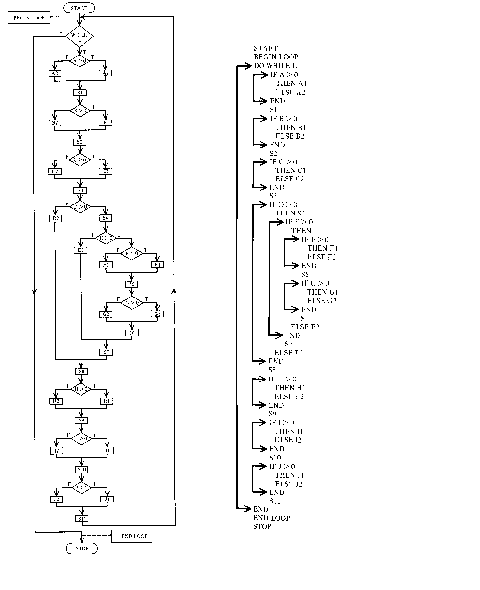
Figure 2.3. Flowchart example from Shooman (1983).
Flowcharts are topological, graph-based constructions that often are filled in with program text. The control logic of the program is shown through simple branches and loops:

Figure 2.3. Flowchart example from Shooman (1983).
In some software methodologies, flowcharts are generated by analysts
as a specification to programmers, who then convert the charts into source
code. In other cases, flowcharts are generated after the fact, either by
hand or automatically.
The usefulness of flowcharts has been hotly debated. Flowcharts for
large systems tend to get large and messy, as decisions can have many branches.
In order to work around this problem, extensions to flow charts allow for
charts to be terminated and then resumed on different pages. Yet, since
flow charts require loops to show return arrows, a program with many loops
requires return arrows that may span many pages.
A structure diagram is a hierarchical, modular breakdown of a program. Between levels on the tree, there are links, with symbols to indicate the sort of information that is being passed back and forth:
Figure 2.4. A structure diagram from Martin (1985).
These structures are represented either as trees or as directed acyclic graphs (DAGs). The structure chart is usually the end result of the activity known as structured analysis, in which the functions of a system are partitioned in a top-down manner. Note the diagrams are purely topological, with labeled edges and nodes. Note also the difficulty apparent in labeling the edges of such a DAG, even on an small example such as the one shown.
At a higher level, the functions of a system are often thought of in
layers, resulting in the following type of diagram:
Figure 2.5. Layer diagram.
This diagram represents that, for this system, an application can access
Motif, X-Lib, a DB API, and a Unix API. If a layer adjoins a layer below
it, then it is allowed to access that adjoining layer.
This sort of diagram will only work on simple access schemes. More complex
schemes will result in a complex graph that cannot be represented with
adjoining regions. The problem is reducible to a planarity problem by considering
regions as nodes and adjoinment as edges; three applications that all can
access three libraries is equivalent to a graph,
known to be non-planar.
Many structured analysis techniques result in trees being generated. An alternate way to represent trees is shown by Warnier-Orr diagrams.

Figure 2.6. A tree structure with its corresponding Warnier-Orr Representation.
Reproduced from Martin(1985).
Instead of the root being at the top, as in a normal tree-structure
breakdown, the root is indicated in the far left corner, and each succeeding
column is at a lower level in the tree. And the use of boxes and lines
is reduced. It is possible to produce a Warnier Orr structure entirely
without lines:
a b
c f
g
d
Figure 2.7. Simplified Warner-Orr Diagram.
constitutes a Warnier-Orr tree representation of the three leftmost
subnodes of A in figure 2.6. Boxes around the nodes and lines between the
nodes are understood - the location of the letter in space implies its
level in a tree structure. Essentially, when programmers indent code to
show nesting structure, a Warnier-Orr convention is being used.
Rothon diagrams attempt to resolve the problems of flowcharts. Rothon
diagrams treat loops as objects without an arrow back to the top of the
loop. Hierarchy is shown by moving left to right through a refinement of
the diagram (Brown 1983).
Figure 2.8. Rothon Diagram. From Brown (1983).
Witty (1977) outlines a flowcharting method very similar to Rothon diagrams. Sequential flow is shown along the vertical axis, and parallel constructs are shown along the horizontal axis. In other words, there is simultaneous control flow along horizontal lines.
Figure 2.9. Dimensional Flow Chart. From Witty (1977).
Diagonal lines are used to show refinement to lower levels of the hierarchy.
One feature of the diagrams is that, on paper, they can be folded up along
refinement lines. When one wants to see detail, one unfolds around the
statement, giving detail. To insert detail into the paper, one cuts the
diagram and insert a new piece.
All flow chart techniques are topological, link-based structures. In
almost all cases, they rely on textual programming language statements
for conditions and assignment statements. The classic flow chart usually
a fairly sparse graph, with most nodes having either one or two outgoing
edges. Back edges in the graph are always from loop statements - a loop
is the visual equivalent of a branch instruction to an previous program
statement. A variety of different node shapes are used to indicate different
forms of computer statement. Each statement in a language, or at least
each statement block, has its own box. For the most part, the charts flow
from top to bottom.
State transition diagrams are well known in computer science as originating from the study of finite automata. Transition diagrams are used for modeling a variety of event-based computer science domains, including parsing, user interface design, and circuit design. At the applications level, they are used to represent transaction flows, appliance controls, marketing scripts, etc. Edges represents transitions from state to state that occur as a result of an input symbol being read.
Figure 2.10. Finite State Automata. From Johnsonbaugh (1984).
State transition diagrams tend to look more graph-like than flow charts,
meaning that there is usually no predefined axis in the diagram. Also,
the degrees of nodes can vary widely, depending on the application. With
the exception of special symbols for start nodes and termination nodes,
all nodes are the same shape. Nodes and edges are both labeled. Termination
nodes are often indicated by two concentric circles - this is to be considered
a different type of node, not an instance of containment.
As state diagrams become large, the chances of the diagram being planar
decreases. Therefore, large state diagrams are unwieldy, with much attention
being required to properly space nodes and edges so that labels can be
read unambiguously. Using the convention of H-graphs (see section 2.3.1),
some of this complexity can be handled:
Figure 2.11. State Chart from Rumbaugh (1991).
This diagram uses a convention devised by Harel (1987) called State
Charts, in which a state such as Forward above, can contain other
states, such as First, Second, Third.
In this sort of diagram, hierarchy is shown using the conventions of
enclosure and adjacency. The figure below shows the Nassi-Schneiderman
representation and the equivalent flow chart.
Figure 2.12. Flow Chart vs. Nassi Schneiderman diagram. From Shu (1988).
Decisions are shown by splitting the line into three smaller, parallel
boxes. Loops are shown by enclosing a box in a larger box labeled with
the loop condition.
As with other adjoinment-based conventions, there is a limit on what
they can represent. The early termination of loops and multiple conditionals
of some languages can be combined in ways that cannot be represented by
these graphs.
In a combination of adjoinment and link-based conventions, data structures
are often showed as adjacent memory locations linked by pointers:
Figure 2.13. Cell and arrow diagram. From Abelson(1985).
Most often this is used for teaching or for program documentation. In programming the manipulation of linked lists, it is customary to think about the manipulation of pointers in a the following manner:
Figure 2.14. Linked list insertion. From Aho (1983).
The accompanying program shows how textual language represents the problem:
procedure insert(x:elementtype; p: position);
var
temp: position;
begin
temp := p^.next;
new(p^.next);
p^.next^.element := x;
P^.next^.next := temp;
end
For the beginning programmer, the program text is confusing
without the corresponding diagram, yet the diagram itself does not contain
enough information to execute from.
Variations on box-and-pointer constructs are often used to represent the displays and activation records of programming languages:
Figure 2.15. Programming language display. From Ghezzi
(1982).
In a kind of static animation, diagrams are often used to explain tree and graph traversals:
Figure 2.16. Tree Traversal. From Aho (1983).
The arrow that shows the sequence of movement we will refer to as a
meta-edge. A meta-edge indicates something about the underlying graph,
and is not part of it.
The representation of data is often accomplished using diagrams. The following diagram shows two different conventions - Entity-Relationship (Chen 1976) and the Object Modeling Technique (Rumbaugh 1991). ER diagrams are extremely simple - there are three sorts of nodes. Entities and Relations form a bipartite graph. Entities and Relations can both have associated Attributes. (A similar convention called conceptual graphs is described in the work of Sowa (1984)).
Figure 2.20. Entity-Relationship and OMT representation. From Rumbaugh (1991).
The Object Modeling Technique uses a convention which allows attributes
to be shown textually, rather than as nodes. More importantly, different
edge types communicate not only the cardinality of relationships, but also
the inheritance characteristics. Note that besides graph conventions, adjoinment
conventions are used to subdivide information in the nodes. Also, heads
and tails of edges are treated as distinct type of nodes with their own
labels.
Figure 2.21. Homomorphism in OMT. From Rumbaugh (1991).
The Object Modeling Technique allows for meta-edges, as in the above
figure, showing the relationship between two different models of data.
The diagram crosses into the symbolic realm through our understanding that
this is really two overlaid diagrams showing two different levels of association.
Figure 2.22. CASE Tool (Software Through Pictures) version of Booch notation. From Fisher (1991).
This diagram from a CASE tool shows a program represented in Booch notation.
In contrast to many of the other diagrams shown, the comparatively low
resolution of screens (75 dots per inch) to paper (300 - 1200 dots per
inch) suggests some of the limits of the amount of information that can
be shown in front of a programmer. Booch notation uses all three conventions:
linkage, enclosure, and adjoinment.
Petri nets are closely related to data flow graphs. The main distinction is that the graphs are bipartite, made up of a set of places and transitions:
Figure 2.23. Petri net. From Johhsonbaugh (1984).
Each type of node can be further subdivided into subtypes.
Figure 2.24. Petri Net node types. From Bauer(1982)
A data flow graph is a directed graph consisting of edges, which represent data flow, and nodes, which represent operations.
Figure 2.25 from
Shu (1988).
Figure 2.26 Roots of a quadratic equation. From Sharp (1985).
Tokens flow through the graph - when a node has tokens ready on all its incoming edges it will execute. When the node has executed, it puts tokens on its output edges. There is no predetermined sequence to the execution of a data flow graph - the data drives the order of execution.
Figure 2.27. Illustration of token firing, from Bauer(1982)
On the graph itself, the nodes can be of 4 types (Perrot 1987) :
computational (2 in, 1 out, or 1 in, 1 out),
control (2 in, 2 out),
merge (2 in, 1 out),
dup (1 in, 2 out).
Dataflow graphs are often used in conjunction with dataflow machines,
computers built to process tokens in parallel.
Dataflow diagrams are oriented to flow-type operations. Objects of data are shown in relationship to procedures. No decision logic is show; the diagram is most often used to model the flow of data.
Figure 2.28. Simple data flow diagram. From Martin (1983).
A simple example is shown above, a more complex example is shown below.
Figure 2.29. Complex data flow diagram. From Gane (1979).
As these diagrams are often complex, an H-graph convention (see section 2.3.1) is often used in which any particular node can expand into subnodes:
The conventions of signal processing are often used to describe streams of computations:
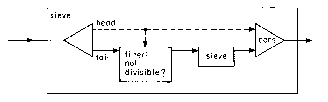
In this example from Abelson, a dotted line indicates a singular element,
while a solid line indicates a stream. Both link and containment conventions
are used. Also, note the use of symbolic recursion; sieve calls itself.
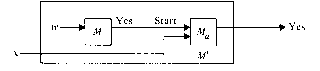
In this example from Hopcroft, the signal processing convention is used
to communicate strategies for combining abstract machines. Again, both
containment and link conventions are used.