All visible objects, man, are but as pasteboard masks...strike, strike through the mask! - Herman Melville	Object-Oriented Design Lecture notes, September 1999 Jeffrey Nickerson
Course Administration Introduction Systems Analysis Design Algebraic Systems Objects Object-Oriented Languages UML Sequence Diagrams Class Diagrams Design Issues Patterns Further Reading One of the early articulators of Systems Theory was Bertalanffy, and this book General Systems Theory is an interesting read, with a good description of how the field was created. Systems Theory originated around the same time as Game Theory, Information Theory, Cybernetics, Decision Theory, and Queuing Theory. For the forecasting of the future is perhaps the basic business of theoretical science; in science it is called prediction. The vehicle for prediction must, to one degree or another, comprise a model for the system under consideration - Rosen, (1985), p 6 an organism, a beehive, an ecosystem also automobiles, cities - all natural systems. We use the adjective "natural" to distinguish these systems from the formal systems which we create to represent and model them; formal systems are the vehicles for drawing inferences from premises, and belong to mathematics rather than science. - Rosen (1985) p 45 Our fundamental awareness of sensory impressions = precepts. We associate the precepts with qualities or properties of the system we are regarding. we assume we don't make them up, so there is an external world. Then a natural system is part of the external world So this system will generate precepts in us, which we will associate with properties of the system itself. Precepts are the fundamental units of experience,... observables are the fundamental units of natural systems - Rosen (1985) 47 A quality corresponds to an observable a quantity corresponds to a specific value of an observable. p 49 So for a system, we need to consider how observables are linked as simultaneous events. How they are related through successor-predecessor relations. We can call these relationships linkages We can't know for sure that what we observe are really linked in the way we think - the system itself doesn't usually tell us "we order food before it appears on the table" So what we really do is build a model, from which we make predictions about what will happen. We create an abstracted system, from which we can make inferences - food ordering before delivery.We call this a formal system, and it is built with mathematical objects. Every design is the expression of a possible future state .. that affects the current state .. through constitution of perceived and acknowledged needs, expectations, and desires. - Nadin The synthesis of form is the crucial step of design. It is when alternative forms are generated. Later, the forms are paired down, analyzed in more depth, and finally one or a couple are chosen for implementation. Experienced good designers can generate more alternatives, and quickly assess them against a number of criteria, including cost.	Every design is the expression of a possible future state.. - M. Nadin Introduction Aristotle found four causes for everything. The fourth one he describes as the final cause - in essence, the purpose. Design is the process of creating things that serve a purpose. We work from the future backwards. Our method is one of generation, refinement, and problem solving, but really we are preparing ourselves for insight. This search for insight, the design activity, is essentially the same in different domains - designers of houses, cities, bridges, carpets, toys, and applications share similar traits and independently have converged on certain ways of working. So long after you have forgotten the syntax of catch and throw in Java, you will still be using the design skills we are focusing on - maybe to design software, maybe for something else. For the next few weeks, I suggest you analyze everything - that you model every bookstore, coffee shop, and gas station you enter. Every elevator bank, every meeting, every purchase. With the goal, the purpose, of working design skills into your system. Systems Systems have an incredibly vague definition, yet we understand what they are. Rosen (Life Itself, p42) describes it this way: These things that belong together, and whatever else depends on them alone, are segregated into a single bag called system; whatever lies outside, like the complement of a set, constitutes environment. So the thing to be clear on is that systems are both living things and mechanical things, large complicated things and very simple things. They can usually best be thought of as a collection of interacting parts. An animal. A cell. And also things more amorphous. A weather system. A society. And the mechanical things we use. A car. An engine system. A computer system. Rosen was a biologist. The reason we are going to follow some of his arguments is that he seems to have thought as hard as anybody about this problem of modeling a system. Biology presents great mysteries that seem to escape normal ways of modeling, and much of Rosen's work leads to some strong conclusions on what constitutes life. We will not follow his argument that far, but we will make use of the distinctions he makes about models. 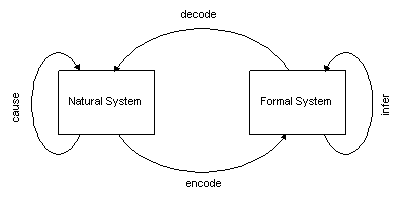Analysis Rosen makes the strong distinction between natural systems and formal systems. Real systems in the external world are natural systems. So even mechanical things are natural systems. Mathematical constructs are formal systems. We sometimes operate on formal systems in the hopes of predicting what the natural system will do. So here is a diagram illustrating Rosen's idea: In the real world, we have physical causes. In the formal world, we have logical inferences. So we might build a model of the weather, and have a rule that says that "where lightening, thunder" and use it to predict the sound of thunder lagging our perception of lightening. Now what if we build a weather simulation program? Is that a natural system or a formal system? If we build it, it is in the external world. So it is a natural system. The process of working from a model to a system in the world Rosen refers to as realization. 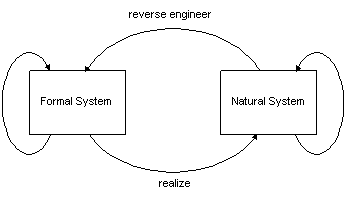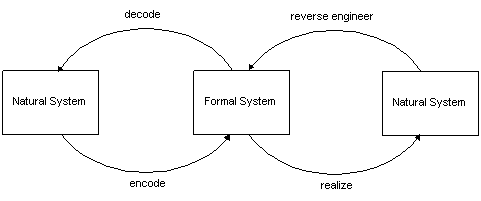The diagram looks the same - we have flipped Formal and Natural, and changed the labels on the arrows: We can tie these diagrams together. Now let's take an example - we are a desert island, and an airplane comes down and lands. We extrapolate a model of aerodynamics from the plane. We look at our model, and realize it doesn't have anything to do with pure size - that all measurements are relative, so we synthesize, we build, we realize a much smaller airplane. Now this is done all the time for wind-tunnel tests. We call those things model airplanes. In our way of talking, we would say the small plane is the realization of a model - and the small plane works to predict the performance of the large plane because it is an analog of the other. In the software world, we have the phenomenon of the clean-room implementations. In order to avoid copyright violations, a company will hire a consultant to observe the behavior of a hardware or software system, and compile a detailed specification. That consultant's contract is then terminated. The specification, the formal model, is then turned over to another set of engineers whose job it is to meet the specification. They have had no exposure to the original project, and cannot be sued for violations of copyright or trademark infringement. The Java Virtual Machine Specification even has the words in it that the document can be used for clean-room implementations. There are a couple of things going on here that deserve attention. The first is that we are saying that the two things on either side of the model, the formal specification, are not the same, yet they behave the same. They behave the same only in the ways we are measuring. In a black-box environment, we are measuring output from a system a property at a time. We probably don't pay attention to all properties. We have built a model that abstracts those things we notice and measure. Rosen calls these things observables. The second thing is that the synthesis step is somewhat mysterious. How do we come up with the system that is 1/6 scale? How did we decide that was better than 1/3 scale or 1/12 scale? Design Synthesis of form is usually taught to architects and engineers in the following way. They are given a design problem, and asked to generate several alternative solutions on paper. They are critiqued, and eventually asked to build something. In an architecture class, they may only be asked to build a scale model. In this class you will be asked to build a program. After you have learned to design. Part of the reason to create a model is that the model is usually easier to manipulate than the system it emulates. So a drawing of a house is easier to change than a house. A sketch of an object model is easier to change than 100,000 lines of software code. Designers get good at manipulating models and coming up with alternative ones. In the software world there are often phases of modeling, so that the overall process looks like this:
Standard software methodologies usually gloss over the most important step - the generation of alternatives, first at the business level, and then at the technical level. Theories come and go, the frog stays - Francois Jacob, cited in Nadin. Dahl, Myhrhaug, and Nygaard invented Simula in 1967	So the creation of a new piece of software may start with the analysis of a manual process, resulting in a model of the way things are currently done. Now we are in the world of formal models, and we manipulate the model, adding, deleting, substituting, until we have generated a few alternative more desirable models, the To Be models. We pick one of these models, which are still very much at the business level, and then generate a number of alternatives for implementing the model. We pick one of these designs, and build the piece of software. Errors Computer systems often mess up. We usually call the problems bugs. These are differences between the model we have in our mind of the way the system should work and the realization. Now the question is where did something go wrong. And it can be anywhere in the diagram. Sometimes what we expected never got put down on paper. Or what we wanted was in conflict with another requirement. Or the implementation does not meet the specification. When an operating system crashes, we know that the implementation is not meeting the spec. And in the case of operating systems it is the shear size of the implementation that prevents all the differences from being removed. Problems discovered later are much more expensive to fix. But problems in a model take more imagination to see than problems in a malfunctioning program. Abstraction An observation procedure applied to a natural system, generates an abstraction. You are measuring one thing - other qualities are ignored. Subsystem A subsystem is a part of a natural system which a small set of observation procedures let us see. So a model is always a subsystem of the corresponding natural system - there is usually something we are not measuring. "The extraction and characterization of subsystems in terms of individual observables, and the employment of such characterizations to encode particular interactions, is the essence of system analysis." Rosen, (1985) 216 Algebraic Systems An algebraic system is a set on which we have an equivalence relation, to be able to tell if elements are the same, and some binary operations associated with it. Often there is an identity element. Along with operations and their corresponding inverses. So we have sets, and operations. Programming languages are mathematical - we have have variables that take on values from sets. Those sets, referred to as types, may, at the basic level, be integers, characters, real numbers, etc. We have pre-supplied operations on those sets - such as + on the integers and the reals. The operations of casting in program languages is about mapping from one set to another, as when we add an integer with a real, the process of converting the integer to the real, adding, and producing a real number as a result. But we also define types. In traditional languages, we define records, which are the Cartesian products of the different domains - in c, struct point {int x, int y} is the Cartesian product x X y. In object languages, we associate with these data records particular operations - so it is really as if we are creating an algebraic system for the type. We define a class - in Java Class Point { private int x; private int y; public void translate(dx, dy) { x = x + dx; y = y + dy; } } z = new Point(); z.translate(3, 4); In theoretical terms, Goguen is writer who best models object-oriented approaches - he describes hidden algebras, that include visible sorts (types) to represent data values, and hidden sorts, for internal states. The object has a signature. A signature is a set of types and a set of operators, each with a given input and output type. An algebra is a signature with a function taking types to sets and another taking operators to functions. State Probably the modern concept of states, especially as they relate to objects, comes from Sir Isaac. In Principia, Newton describes particle systems. If you know the displacement and momenta of the particles at an instant of time you can describe the entire state of the system. And if you have forces together with initial values of the state variables you can determine the state variables, and every other systems quantity, for all time. "An impressed force is an action exerted upon a body, in order to change its state, either of reset, or of uniform motion in a right line" Newton, p2. Newton's first Law of Motion Every body continues in its state of rest, or of uniform motion in a straight line, unless it is compelled to change that state by forces impressed upon it. Objects In order to get the idea of objects, think of an appliance - let's take a CD player. It has states, constituted by these attributes: On, off Volume battery level It has public outside operations: load CD. unload, Play, pause, change volume, load battery, plug in, fast forward. It also has a set of invisible operations that only the engineers know about: spinning up to speed, cutting off volume above a certain level, powering down automatically after a certain idle time. The interface for playing a CD, a video, a DVD is becoming standard - you can imagine that as designers, you just take for granted you will have buttons with certain labels indicating fast forward, pause, stop, rewind. This is what the interface convention of UML (and Java) can be used for: define a standard interface, and worry about how to implement it later. As a user, you only have to learn the interface once, and it will work on many different objects. OO languages The first OO language came from a set of Norwegians who wanted to build a simulation language. The language, they thought, would help us understand the world better. It was named Simula. And it was really used initially to try to simulate societal types of issues. Queuing theory was a big influence on the language - so the language was good at doing things like mimicking the wait at a bank for the next teller. Almost all the good object ideas go back to 1967. Smalltalk added a very important idea - that a graphic user interface is made up of sets of objects. We send messages to these objects by manipulating them with a mouse and a keyboard. C++ drew on Simula, and Java combined ideas from all the previous OO languages.
. UML text: Peter Coad et al, Java Design, 2nd Edition, Yourdon Press, 1999 Different types of UML diagrams: Sequence, Class, State, Activity, Collaboration, Use Case, Object, Package, Component, Deployment Here is a good UML reference site Scott Ambler's article on UML modeling of architecture is worth reading. Here is the Rational UML Quickreference - it is worth printing. And a UML primer Other recommended texts are those by Rumbaugh, Booch, and Jacobson, who are responsible for UML, as well as all texts by Coad.	Visualizing Object Designs Even though OO started in the 60s, it wasn't until the late 80s that standard ways of visualizing objects began appearing. But, to be fair, some other techniques, such as Entity-Relationship Modeling , are very close in concept to object modeling. In some ways, OO modeling is a co-opting of a variety of analytic diagrams that go way back. For more on visualization, see this chapter of my thesis. The Unified Modeling Language (UML) UML is a standard modeling convention, created to stop industry bickering and create a larger market for Computer-Aided Software Engineering tools based on Object-Oriented techniques. The current set of conventions in UML come from a number of different sources. There are at least 9 different diagram conventions that are part of the modeling language. And there are case tools such as Rational Rose that will allow you to create diagrams, move from diagrams to code, and then reverse-engineer back to diagrams. For the purpose of this course, UML is a tool - I am not going to teach every aspect of the different diagrams. I don't think all of them are useful. I do want you to be facile with the few diagram conventions I present here. By the way, the Coad book takes a similar approach, only using a subset of UML conventions. 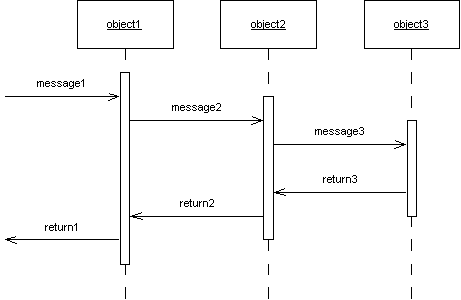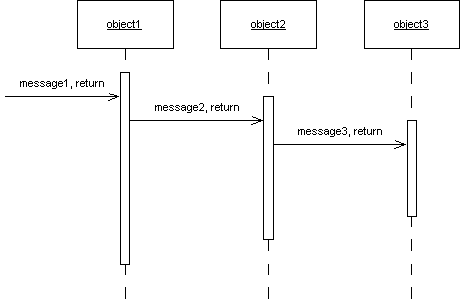Sequence Diagrams In my mind, this is the most useful software diagram, period. Across the top we have objects. Between them we show messages. The extent of an objects control is shown by the vertical rectangle. There are two alternative conventions for showing returning messages - show them explicitly, or make them implicit in the way the message is passed back and forth. 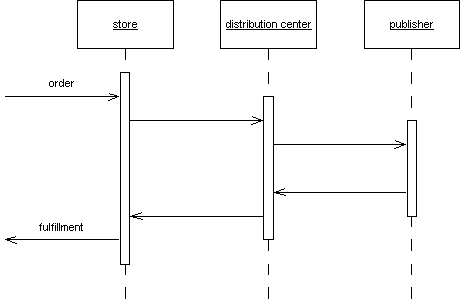You can see the two diagrams above are equivalent. Coad uses the later convention, in the following way: The method name passes two parameters, the input and the output. In this case, an interface object is passing a name to a lookup object that will return a corresponding phone number. Now, I want to be clear that these diagrams work even at the level of business analysis. Here we look at an online bookstore - an order comes in for a book that in this case is not present in the distribution center, so the publisher is contacted. The total time for the transaction is high for the customer. But the store doesn't need to keep any inventory. In the following diagram, the distribution center anticipates a customer order, and fills up on stock. The store anticipates the customer order. The customer gets a quick transaction, but the bookstore has to hold inventory. Sequence diagrams apply at any level of systems - the things in the top boxes can be people or large software systems, or they can be 10 line Java-coded objects. 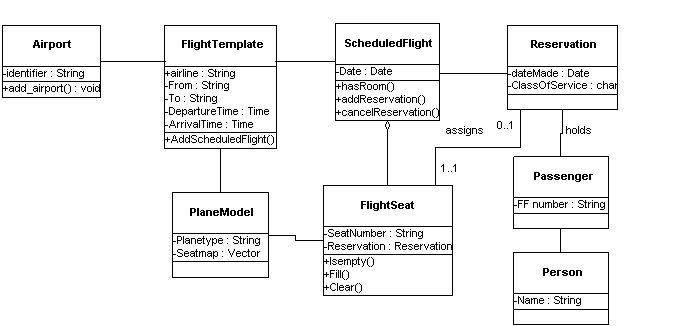Class Diagrams For those of you who have been involved in database design, class diagrams will be very familiar. They look almost identical to entity-relationship diagrams. The major difference is that not only data attributes, but also operations are shown. This diagram is based on the one in Coad on page 25 - but I have added two classes, PlaneModel and Seat.
"In the last resort, structure (i.e., order of parts) and function (order of processes) may be the very same things." p27 Bertalanffy. patterns	Notice that there is a relationship between sequence diagrams and class diagrams. Every arrow on sequence diagram that points toward an object is reflected as an operation of that object on this diagram. Notice that the associations, however, have nothing to do with the sequence diagram - just because an object calls another object doesn't mean there is a structural association between the two. Think of time and space, with the class diagram representing static relationships that define the structure of the domain. From the right level of class diagram, it is possible to generate code stubs. The CD in the back of the Java Design book contains a CASE program that will allow you to create a class diagram, and from it, generate Java. It will even work the other direction. The crucial decision the case tool will make is how to encode the association links of the diagram. For this it will work off the cardinality information that you can provide it. The way to keep cardinality straight is to think it through in two steps, from the perspective of each object. "If I am a reservation, how many seats do I associate with" which we have answered with a 1. "If I am a seat, how many reservations do I have associated with me" - which we have answered with a zero or 1. Now notice that we have an assumption here - we are somehow going to have to generate a new seat object for each scheduled flight. So probably in the addScheduledFlight method, we would go to the PlaneModel object, and create a new seat according the floorplan of, say, the Boeing 747. Then part of implementation will involve traversing this set of seats to figure out which seats are reserved and which passengers have checked in. Our interface ought to show a map to an agent who is trying to decide where to put passengers. There is another unusual feature of this diagram - the diamond shape shows aggregation, which can be read "part of". The seats are part of the flight. If the flight is canceled, the seats disappear. By the way, the huge association usually discussed in object-oriented design is inheritance, which is a "kind of" relationship. You need to understand it, as a lot of the Java libraries are based on it. But in actual analysis it is not always that useful, and in coding it can quickly become very complicated. The treatment of inheritance and its alternatives in Coad, chapter 2, is very good. In particular, it is useful to understand than the inheritance tree of a Java applet goes like this: Applet -> Panel -> Container -> Component -> Object. So when we create an applet, we can inherit from applet, which already has a large set of pre-defined methods. We don't have to bother to write special methods for resizing the window, unless there is something out of the ordinary we want to do. Design Issues When do you go from analysis to design? When you stop being concerned with the present situation and start to motivate yourself for action. But the boundary is not so clear - your analysis has a motivation, which is usually to understand a present state so your future state will fulfill the implicit requirements of the current environment. A typical user requirement: "I want it to do everything it does now, but these additional thing, and a lot faster, without any of the current drawbacks, and I want the new system to be inexpensive, delivered soon, and be flawless". There is an economics of design. The above requirement overconstrains the problem - there will be no solution. You can either decide not to build it, or pick which requirements to ignore. Patterns The point of studying systems is that what you learn on one system seems to apply by analogy to another system. So a good designer recognizes patterns, and focuses straight in on the pivotal issue of a problem Many attempts are being made to catalog patterns used in software design. Most efforts are not very useful - I would categorize them as attempts to make archetypal overly clever constructs. The exception is Coad - his books do analyze situations that continue to recur in business systems. Patterns only go so far - software design is interesting because you can create something new. And that newness is usually the result of practice in manipulating models in your mind.
	Further reading The bibliography of works discussed on this page A systems bibliography A deep thinker on objects: Goguen Algebraic Semiotics Also from Goguen, known for his applications of category theory to software. BLENDING AND CONCEPTUAL INTEGRATION  This is also discussed in Goguen, above Robert Rosen's work.  Mind - Wuppertal- Interesting work from Germany, the product of Nadin. Metaphor in Scientific Thinking Page
Philosophy may be ignored but not escaped; and those who most ignore least escape - David Hawkins, cited in Rosen	Course Administration Lecture text: Peter Coad et al, Java Design, 2nd Edition, Yourdon Press, 1999. Reading Assignments: By the second Lecture, Chapters 1-3. By the third Lecture, Chapters 4-5. Assignment for the second lecture Group exercise - create alternative business models around the subject given, choose one consider 3 alternative project scopes choose one, create sequence diagrams for at least 3 use-cases create a class diagram individual exercise - The same as above, but choose a different design domain. Suggested domains: A pizza parlor point-of-sale system. An online record store A new york ferry simulation. A genetic algorithm toolkit An elevators in a sky-scraper simulation A personal organization system for all books, records, course notes, files, magazines, mapping them physical locations in your home. Assignment for lecture 3: Group Assignment The generation of 5 different physical architectures for your project, and the sketching out of physical details for one architecture. Individual assignment Class diagrams and Java class definitions/stubs for the project of your choice - preferably the one you worked on for lecture 2.
	Email to the lecturer: jeff@nickerson.to